RIP Algorithm

Let's look at what happens when a datagram is sent from one source to a destination. If the source and the destination are in the same autonomous system it is delivered by the system's technology. But, if the destination is in another autonomous system the datagram should be transferred to that autonomous system. There it will be delivered by that system technology. routers are the ones that should do the transferring. Therefore, they should know all the autonomous systems in the supernet. When they receive a datagram addressed to autonomous system `A' they should transfer it to `A'. A trivial way to implement a router is having one router that is connected to all autonomous systems. However this is not practical. A more practical way is having many routers. Each connected to few autonomous systems. Let a datagram be sent from one autonomous system to another. The router of the first autonomous system would transfer the datagram to that autonomous system (if it can), or transfer it to another router, that knows how to reach the destination. Eventually the datagram will reach a router that has a connection to that autonomous system and the datagram will be transferred correctly.

This way requires each router to hold a database of all the possible destinations. Each entry in the database should hold the next router that datagrams should be sent to. This way could have worked very well. Alas, the network cannot be kept still. New routers can be installed Old routers can crash. Crashed router can come up. Therefore, our connection through a router is not guaranteed. Even if the router doesn't crash, a new router may be installed, providing better service.

Before we continue this discussion, we have to make few things clearer. We have to define what we mean by saying that one line is better than the other. There are many ways to measure a connections. You can measure it by the Dollar cost, number of hops in the way, error rate, latency, etc. We will assume that connection are measured by the number of hops in its path. This assumption is no way, obligatory and any system administrator can define a measure of his own. We will treat measure as costs. That means that the lower the number associated with the connection, the better. RIP treats any number higher than fifteen as infinity (sixteen). So, sixteen means 'no connection'. This method of calculating the cost is called metric.

Let d( i , j ) be the cost of the direct link from i to j .

d( i , i ) = 0 for any i .

Let D( i , j ) be the cost of the best route from i to j . It is defined for any two entities i , j .

D( i , i ) = 0 for any i .

D( i , j ) = min [d( i , k ) + D( k , j )] for i <> j

The last equation can be proven using induction over the number of steps in the routes. The metrics can be calculated using a simple algorithm. Entity i gets its neighbor k to send their estimates of their distance from j . When i gets the estimates from k , it adds d( i , k ) to each of the numbers. Then i picks the smallest value. A proof that this algorithm converges to the correct values of D( i , j ) in finite time, when the network topology does not change. Very few assumption were made about the order in which the entities send each other their information. No assumption were made on the initial values of D( i , j ), except that they have to be non-negative. That means that it is safe to run the algorithm asynchronously. Entities can send updates by their own clock. Updates may be dropped, as long as they don't get all dropped. Because there are no assumptions on the initials values, the algorithm handles changes. when the topology changes, the system will move to a new equilibrium using the old one as its starting point.

Once a router is installed, or started, it should send messages to all of its neighbors. This is necessary in order to update their tables. Consider this case:

A was connected to D through B and C . Once E has been installed, A can connect to D through E . This line costs less. That's why E has to announce its existence to A . If E should ever crash, A must know about it. Otherwise it will continue to send datagram s through E . Unfortunately, a router can't always inform others, that it is about to crash. A router can't depend on such message to warn it. Therefore a router crash, must be learned in other ways. RIP forces a router to send update messages every thirty seconds. These messages contain routes, that that router knows; and their metrics. If a router does not receive an update message for 180 seconds. from another router. It assumes that router to be unreachable. This timeout of 180 seconds allow a router to miss five update messages, without being marked unreachable. This is necessary, because the media might be unreliable and loose datagrams.

The algorithm so far, sends update messages every thirty seconds. Every update message contains a list of the autonomous system the routers knows to reach and their metrics. If the metric in an update message is lower than the metric in the router 's table, the router would update the metric and the next hop fields in its table. If for some destination, an update had come from the next hop, indicating a different metric, then the metric in the table should be changed. This is necessary because if the metric changes in the next hop, we must change the metric in our router, as well. This guarantees correct performance, but not good enough. Consider this case:

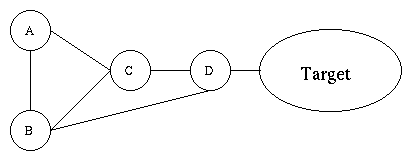
All links have cost of 1, except for the direct link from C to B which has cost 10. Each router will have a table showing the next hop and the metric for each destination. We're interested only in the connection to the target network.

D : directly connected, metric 1.

B : connected via D , metric 2.

C : connected via B , metric 3.

A : connected via B , metric 3.

Now suppose that the link from B to D fails. The routes should adjust to use the link from C to D . Unfortunately it will take quite a while for this to happen. The routing changes start when B notices that the route to D is no longer usable. The chart below assumes that all router s send updates at the same time. the chart shows the metrics for the target.

time ---> 

 B : unreachable |  C , 4 |   C , 5   .... 

 C :  B ,  3     |  A , 4 |   A , 5 

 A :  B ,  3     |  C , 4 |   C , 5 


The problem is that A and C both believe they can connect to the target through each other. 
It happened because they sent messages indicating they can connect to the target at cost of 3. When they received 
the message from B saying that the target is unreachable, they received another message. The second message 
said they can connect to the target in cost of 3. This cost is of course not true, because the link from B
to D is unusable. Since A and C don't know that the route from each other uses another 
link that is no longer usable, they would both update their tables to point at each other. Since, they increase 
the metric by one, they will both report that the cost is now four. Since A uses C as next connection, 
and C signals that the cost had change, A would change the cost of the link. Same thing would happen 
to C . This way the cost of the connection will slowly rise. The worst case is when the target is really unusable, 
and then the cost will rise up to infinity. This effect is called 'counting to infinity'. This is why infinity was 
chosen to be such a small number. If some autonomous system becomes completely unreachable, 
we would like the counting to be over as soon as possible.

There are several ways to prevent this from happening. The ones that RIP uses are called 'split horizon with poison reverse' and 'triggered update'.

Split horizon.

Notice that the problem above is caused because both A and C deceive each other. They both claim they have a connection. Since they both think they can connect through each other, a real link is not established. This could have been prevented if A hadn't told C that it can connect to the target. Generally, it is not useful to claim reachability for a destination to the neighbor from which the route was learned. The "simple split horizon" omits routes learned from one neighbor in updates to that neighbor. "split horizon with poisoned reverse" include those routes but with cost of infinity.

If A thinks it can get to D through C its message to C should indicate that D is unreachable. If C still claim reachability to D , then either it is connected directly to D , or it knows another router that claim reachability. C 's route to the destination cannot go back to any route that points to C .

In general, split horizon with poisoned reverse, is safer than simple split horizon. If two routers point at each other, advertising reverse routes with metric of 16 will brake the loop immediately. If the reverse routes are simply omitted, those routes will have to be eliminated by waiting for a timeout. Alas, poisoned reverse increases the size of the messages. Consider the case of a campus backbone connecting many buildings. Each building has a router. In simple split horizon only the network that is connected to the router is included in the updates messages. In split horizon with poisoned reverse, ALL networks learned must be published as well.

Implementors may use simple split horizon if they like. Or they can offer a configuration option, to allow the system manager to choose which way to use. It is also possible to advertise some reverse routes with metric of sixteen, and omit others.

Triggered updates.

Split horizon with poisoned reverse will break any loop of two router s. However, it is still possible for loops of three or more router s, to occur. A may think it can reach the target through B . B may think it can reach the target through C . C may think it can reach the target through A . This loop will break only when infinity will be reached. Triggered updates are an attempt to speed up this convergence. To imply triggered updates, we simply add a rule that whenever a router changes the metric of a route, it is required to send update messages almost immediately. The triggered update messages will be sent even if it is not time to the regular update message. Consider a case were G can connect to a target network, and then its link becomes unusable. G will send its neighbor updates about the change. Its neighbors will update their tables if necessary. The ones that updated their tables will send their own update messages. Some of the neighbors' neighbors will update their tables, and send their own update messages. The update messages will propagate back, until they reach a portion of the network that uses another route to connect to the target.

If the system could be made to stay still while the update messages propagate back, it had been possible to prove that counting to infinity would never happen. A bad router will be removed from the tables, using update messages. Alas, this is not the case. While the triggered updates are being sent, regular updates can be sent, from router who hasn't got the update yet. Their update will indicate that the target is still reachable. It is possible that a router will receive a false regular update saying the target is reachable, after it received a triggered update saying the target is unreachable. This could reestablish a connection incorrectly. Triggered updates reduce the chance to get counting to infinity, however this can still happen.